• Problem Definition
• Mixed Density Networks
  • How does it look like?
• Long Short Term Memory Networks
• Model(LSTM + MDN)
• Loss Function

As everyone comes up with a resolution at the start of the year, I would be trying to be more infrequent in my blog postings😀. As it has been over a month, I thought of spilling some words here 😀. In this blog, we will be discussing about an interesting paper on Generating Sequences With Recurrent Neural Networks proposed by Alex Graves(DeepMind). I will also be implementing the paper using Tensorflow and Keras.

Problem Definition

The dataset here is in the form of mathematical representation of handwritten strokes. So a point in the stroke sequence is a vector of length=3. First value is a binary digit denoting whether the pen lifts in the air at the point or not. Second value is the offset of the x coodinate relative to the previous x-value in the sequence and similarly the third value is the offset in the y coordinate. The problem is, given the dataset, we need a model which can generate handwritten strokes unconditionally(randomly by giving a seed value, just like GANs).

Mixed Density Networks

Before moving into the implementation part, I would like to discuss about a special kind of network called MDNs or Mixed Density Networks. The goal of a supervised problem is to model a generator or a joint probability distribution over the features and the labels. But in most of the cases the distributions are considered to be time-invariant such as in the cases of image or text classification. But when the probability distribution itself is non-stationary as in cases like handwritten strokes or say path coordinates of a car, normal neural networks perform very badly there. Mixed Density Networks assume the dataset to be a mixture of various distributions and tends to learn the statistical parameters of those distributions resulting in better performance. CONFUSED?

Okay fine, we are going to get into more details.

Let us take an example shown in the figure below:

In the first figure, given the Θ1 and Θ2, when asked about predicting the position of robotic arm, we have a unique solution. Now, look at the second figure, the problem has been reversed. Given the x1 and x2, when asked about predicting the Θ parameters, we get two solutions. In most of the cases, we get a problem like the first figure where the data distribution can be assumed to come from a single gaussian distribution. While for the case like the second figure, if we use the conventional neural networks, it does not go down well with the performance. I will tell you why, shortly.

It is not that neural networks having mean squared losses or cross entropy losses do not consider the (mixture of distributions) thing. It considers that thing, but gives a resulting distribution which is the mean of all those mixtures and this paper suggests that we do not need the mean and instead the most probable mixture component to model the statistical parameters. And thus MDN comes into picture.

How does it look like?

So MDN is nothing but a neural network predicting the statistical parameters instead the probabilities for the classes or values for a regression problem. Let us assume the data to be a mixture of M normal distributions, so the final prediction will be M probabilities weights for the mixtures, M mean values and M variances. And while sampling we take the parameters of the most probable mixture component. We will talk more about the structure and implementations later.

Long Short Term Memory Networks

While it is not a new thing, I may expect some new people. So I will give a basic idea about LSTMs here. So, LSTMs are nothing but a special kind of neural network having three gates, input, foget and output gates respectively. The most important thing in a LSTM cell is its memory C shown in the figure above.

Forget Gate: A LSTM cell will output the hidden state and the memory of its cell which fed to the cell next to it. A forget gate decides the amount of the information from the previous memory to be passed into the current cell. It basically takes the previous output and current input and outputs a forget probability.

Input Gate: It takes the same inputs as the forget gate and outputs a probability which decides the amount of information of the cell state which contributes to its memory.

Output Gate: It again takes the same inputs as above and gives a probability which predicts a probability to decide the amount of information to be passes to its next cell.

LSTMs are quite good at handling sequential inputs like texts, time-series datasets or stroke datasets discussed earlier and give a robust feature vector for a sample data sequence. Alex Graves thus proposes to use them for the handwritten strokes to find a feature vector for a stroke sequence which is then fed to a MDN network to find the statistical parameters as shown in the figure below:

I hope we are now good to get into the implementation part. I will use Keras to create the network and Tensorflow at its backend to define the loss function.

It is assumed that the x and y point offsets follow mixture of bivariate normal distributions and the penlifts follow a bernoulli distribution(obvious, right?). I will demostrate the solution using a mixture of 2 bivariate normal distributions and bernoulli distribution can be parametrized by a single probability value, right?

Oh! I forgot to tell you about the loss function. It is defined by the equation given below:

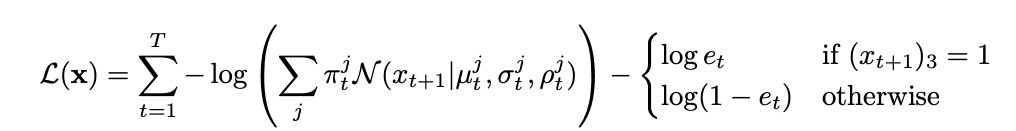
where π is the probability of mixture components and e is the probability of the end of stroke which parametrizes the bernoulli distribution.

Now let us do the task we are hired for 😮….🤫….😃 Code Code Code:

The input will be a sequence of 3 length vectors and output of each point is the next point in the stroke sequence like shown in the figure below:

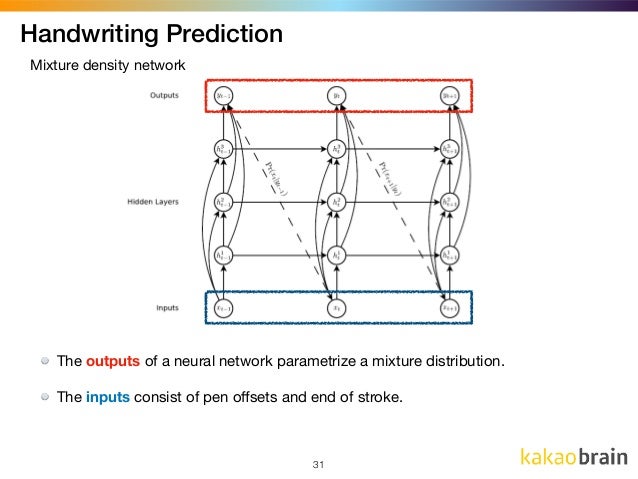
Model(LSTM + MDN)

import numpy as np
import numpy
import tensorflow as tf
import tensorflow.keras as keras
import tensorflow.keras.backend as K
import keras.layers.Input as Input
import keras.layers.LSTM as LSTM
from tensorflow.keras.models import Model

# nout = 1 eos + 2 mixture weights + 2*2 means \
# + 2*2 variances + 2 correlations for bivariates

def build_model(ninp=3, nmix=2):
    inp = Input(shape=(None, ninp), dtype='float32')
    l,h,c = LSTM(400, return_sequences=True, \
    return_state=True)(inp)
    l1 ,_,_= LSTM(400, return_sequences=True, \
    return_state=True)(l, initial_state=[h,c])
    
    output = keras.layers.Dense(nmix*6 + 1)(l1)
    model = Model(inp,output)
    
    return model

Loss Function

def seqloss():
    def pdf(x1, x2, mu1, mu2, s1, s2,rho):
        norm1 = tf.subtract(x1, mu1)
        norm2 = tf.subtract(x2, mu2)
        s1s2 = tf.multiply(s1, s2)
        z = tf.square(tf.div(norm1, s1)) + \
            tf.square(tf.div(norm2, s2)) - \
            2 * tf.div(tf.multiply(rho, tf.multiply(norm1, norm2)), s1s2)
        negRho = 1 - tf.square(rho)
        result = tf.exp(tf.div(-z, 2 * negRho))
        denom = 2 * np.pi * tf.multiply(s1s2, tf.sqrt(negRho))
        result = tf.div(result, denom)
        return result
        
    def loss(y_true, pred):
    
        prob = K.sigmoid(pred[0][:,0]); pi = K.softmax(pred[0][:,1:3])
        
        x = y_true[0][:,1]; y = y_true[0][:,2]; penlifts = y_true[0][:,0]
        
        m11 = K.sigmoid(pred[0][:,3]); m12 = K.sigmoid(pred[0][:,4])
        s11= K.exp(pred[0][:,5]); s12 = K.exp(pred[0][:,6])
        rho1 = K.tanh(pred[0][:,7])
        pdf1 = tf.maximum(tf.multiply(pdf(x, y, m11, m12, s11, s12, rho1),pi[:,0]), K.epsilon())
        
        for i in range(1,2):
            m11 = K.sigmoid(pred[0][:,3+5*i]); m12 = K.sigmoid(pred[0][:,4+5*i])
            s11 = K.exp(pred[0][:,5+5*i]); s12 = K.exp(pred[0][:,6+5*i])
            rho1 = K.tanh(pred[0][:,7+5*i])
            pdf1 += tf.maximum(tf.multiply(pdf(x, y, m11, m12, s11, s12, rho1),pi[:,i]), K.epsilon())

        
        loss1 = tf.math.reduce_sum(-tf.log(pdf1))
        pos = tf.multiply(prob, penlifts)
        neg = tf.multiply(1-prob, 1-penlifts)
        loss2 = tf.math.reduce_mean(-tf.log(pos+neg))
        final_loss = loss1+loss2
        
        return final_loss

    return loss

I trained the model for 2 epochs on a small dataset of strokes stochastically because the lengths of strokes were varying. The results I got looks like the one shown below:

I suppose if you increase the number of mixtures and dataset and epochs collectively or individually, you will get better results. I hope the blog was an enjoyable read and please reach out to me if you have any doubts or suggestions.

Keep Learning, Keep Sharing