• Incremental Learning
  • Limitations of Transfer Learning
  • Revise and Learn
  • A Necessary Naive One 👇🏻
  • Pseudo-Revision 🙄
  • Knowledge Distillation-Loss
• Algorithm

One of the major area of concern in deep learning is the generalisation problem. This has been a hot topic for research for the past few years. Generally what happens is that we get a use case, we build a model for that and we push it in production. But what if we have a slight change in our problem statement. Do we need to solve it once again from the scratch? What if we dont have the dataset we had previously? We seek for a way to preserve the previous learning of the system and work on just the evolution part. And we will be talking about one of the similar aspects of the problem in this blog. So, welcome to the new blog of Learn & Share thread and bear with me for some of the next few paragraphs.

Incremental Learning

Let us define the problem statement first and then we shall discuss the various solutions for that. Suppose you have a dataset for 5 classes and you built a deep learning network for the classification problem. Now, let us imagine you have the model but you lost the dataset and you need to add an extra class for the existing problem statement. Well, let us not get to the solution that quickly. Instead, let us derive the solution from the history itself.

One of the famous start in the approaches of generalisation is Transfer Learning which has infact proved to be very successful. So, in this approach we already have a pre-trained model for a dataset1. Now, if a new dataset2, which comes from a similar kind of domain, we can use the knowledge of the previous pre-trained model instead of training it again from scratch. What happens is that we initialise the new model with the same weights as of the pre-trained model and add a new softmax layer removing the last layer of the previous model(cosidering it is a classification problem). And we train the model, starting from the point where the pre-trained model had reached already. This results in fast and better convergence. If the previous model is very large, we do not have to update the weights for its previous layers(you can decide how many) by freezing them(making them untrainable). We update only the weights of the extra layers(some previous layers too if you want) we have added. This strategy is called Fine Tuning.

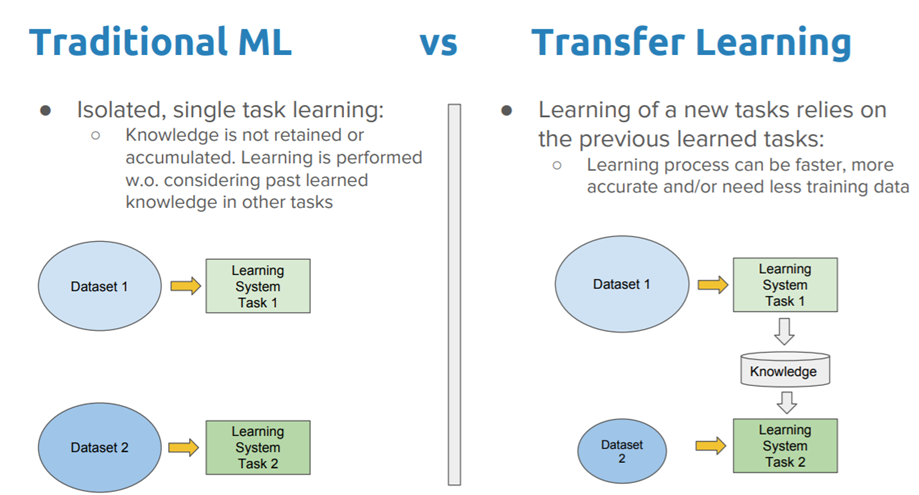
Limitations of Transfer Learning

The limitation of Transfer learning is that it can not be used for incremental learning if we do not have the dataset for the previous classes. Confused? 🤔 Let us understand it by an example: Suppose the pre-trained model used the dataset1 which had classes -> {A, B, C, D}. Now we need to add some extra classes, let us say {E, F, G} to model. The obvious approach would be to remove the previous softmax layer having 4 output nodes and add a new one with 7 output nodes and fine-tune the model with new dataset consisting of classes -> {E, F, G}. Well, if you do that, you will get very bad accuracy for the previous classes(may be for the new classes too). This is the major problem we will be talking about from here now and it is called Catastrophic Forgetting by neural networks.

Revise and Learn

We humans are very good at generalisation because we have some sort of memory network in our brain which stores the previous knowledge and fine-tune it according to the new tasks we get exposed to. The important thing is that we do not deviate much from our previous learning. Neural Networks are very basic and simple prototypes of real neurons and it still is challenging to reach to that level. In our previous problem, if we have the previous dataset1 and we combine it with the new dataset2 to reach our final objective, we surely get a good result. That is because the dataset1 lets the neural network revise its knowledge and avoides it from deviating too much. The dataset2 on the other hand allows the neural network to fine-tune itself for learning new classes. So, is having the entire dataset the only solution? IT IS NOT 😀. Let us discuss the possible solutions one by one:

A Necessary Naive One 👇🏻

As the name suggests, it does not go well with the performance but still it is good to know the naive ones for achieving a better solution. Remember, we talked about not letting our neural network from deviating too much. So one obvious thing for that would be to add a regularizing constraint on the weights of the pre-trained model to prevent it from going too far. The reason it does not work because in neural networks, generally we have more number of weights than the entire data points and thus they learn functions which are highly complicated and far away from being linear. So even a small amount of change in the weights could allow the new final objective function to go farther from the old one. No worries, have patience. We have a better solution coming next👇🏻

Pseudo-Revision 🙄

If you recall, we talked about revising old things before learning the new ones. So, the idea here is to obtain something which can be used for the revision for our pretrained-model. And this is what a research proposed by Zhizhong Li et al does.

The revision part is done by the dataset2 only but with a different strategy. As it is known that even if a data-point does not belong to the trained classes, a neural network will predict some probabilities for each of those classes. The predicted probabilities for the old classes act as the old labels in the new-training now. The aim is to obtain a similar kind of probabilty distribution which the old model would have predicted for the new dataset2.

Knowledge Distillation-Loss

The loss function used for the old task will be a modified cross-entropy with the probabilties altered according to the definition given by Hinton et al. The idea here is to increase the weights for the low probabilities for better encoding of similarities among the classes. The loss function can be mathematically represented as follows:

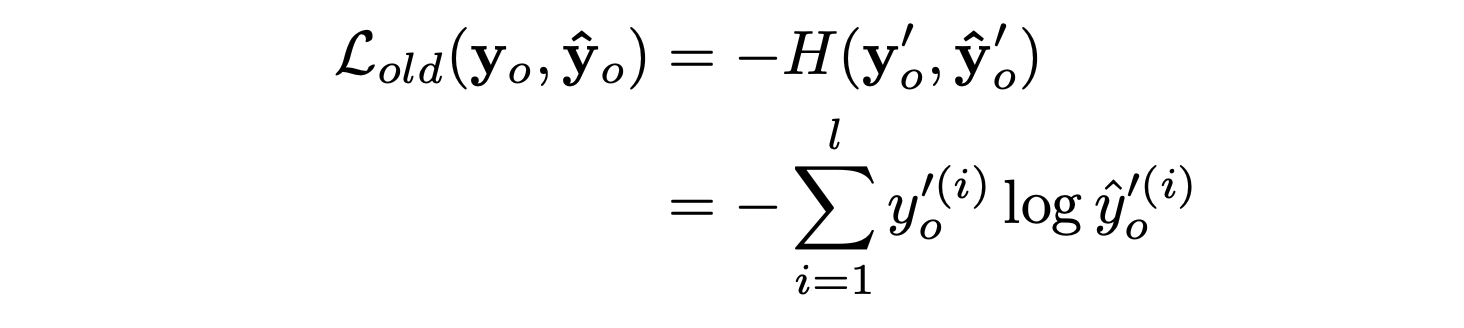
where,

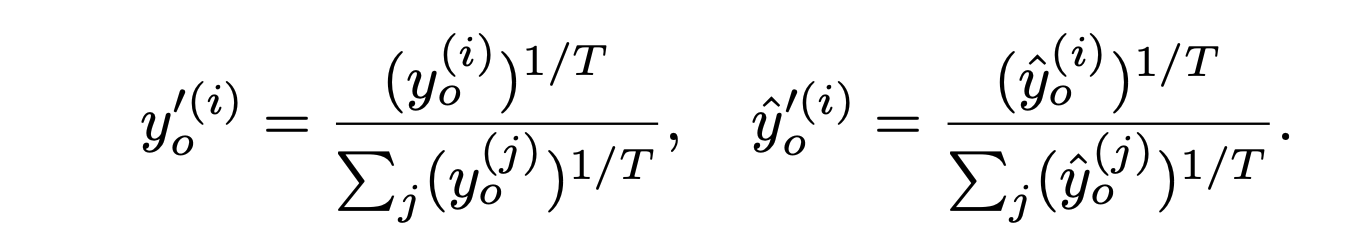
T is a constant greater than or equal to 1. For the new tasks, we use the usual categorical cross-entropy loss.

Algorithm

Now that we have understood about the loss functions and the basic idea behind the research. Let us discuss the end to end algorithm:

Step 1: Obtain probabilities for old task by feeding the dataset2 to the old model Step 2: Randomly initialise the weights of new layers that you have added.

During training we have three losses:

1. Loss for old task : L_old
   
2. Loss for new task : L_new
   
3. Regularization for the weights

To control the importance for the losses, the total loss is a weighted sum of the three losses mentioned above with λ_old as the weight for the old task loss, λ_new as the weight for the new task loss and λ_r as the regularizer constant.

The above algorithm gives us good performance but again the multi task transfer learning approach with data for every class stands above when performance is considered.

I hope the blog gives an informative insight about incremental learning. I will keep adding more algorithms as I keep learning about them.

Till then, Keep Learning, Keep Sharing