Recently, I started studying Reinforcement Learning and was fascinated by the potential it possesses. In this blog, we will have a quick discussion over the terms, Q-Learning and OpenAI gym library. Finally, we will be implementing a simple Q-Learning application on one of the gym environments.

Let us start with Q-Learning:

Q-Learning is an algorithm designed to find the best possible decision to take, given a current state. Let us imagine what a child will do if it is just kept at a random state and somewhere around it, lies a bar of chocolate. The child will try many times to stand, crawl, fail many times and ultimately will get the chocolate. This is similar to what a q-learning algorithm does. An agent is exposed to a surrounding completely unknown to it. It takes some random actions, gets the reward or punishment due to those actions and learns to take further decisions.

You may be wondering if it does the same thing as supervised learning. The answer is NO. In reinforcement learning, evaluative learning happens whereas in supervised case, it is instructive. Meaning, in supervised learning, weights are updated using the pre-defined labels, so that the model does not predict the wrong class further. While in reinforcement learning, the agent tries every possible action and can keep predicting the wrong class if it is getting a higher reward for it and goes for the right class once it finds it.

Mathematically, it can be defined as follows:

The above equation tells us how we update a q-table. We need to understand the term q-table obviously here. q-table can be considered as a matrix having values for each {state, action} pair. When in a particular state, the agent will take the action which corresponds to the maximum value. Initialising the q-table depends upon the heuristics the same as in the case of neural-network weights. We can update the values of the q-table(q-values) by the equation given above.

Alpha is the learning rate having a value between 0 and 1. The discount factor gamma is also a value between 0 and 1 but is typically kept high as it shows how much does the q-value of future decision affects the current q-value. R(s, a) is the reward the agent gets for taking an action, a being in a state, s. maxQ’(s’, a’) is the maximum reward to be expected by considering all possible actions in the new state, s’.

Now, let us talk about gym. It is a library provided by OpenAI which simulates various environments and plots them which helps us visualise our q-learning algorithm easily.

It can be installed by running the following command:

$ pip install gym

You must ensure that matplotlib is also installed in your system. If not, you can do it by running the command given below:

$ pip install matplotlib

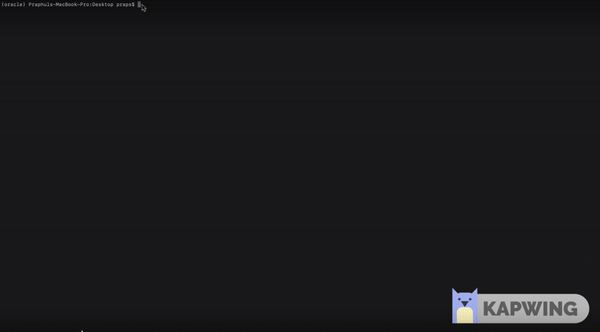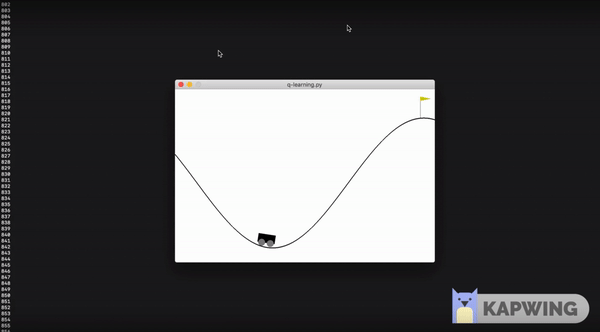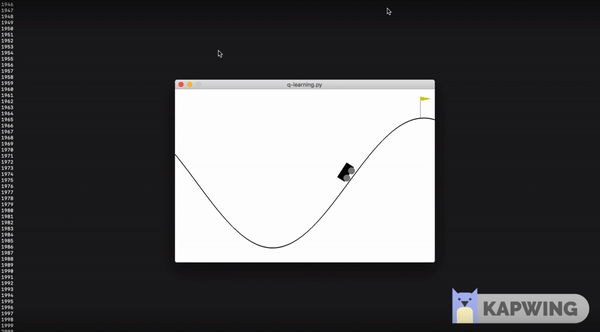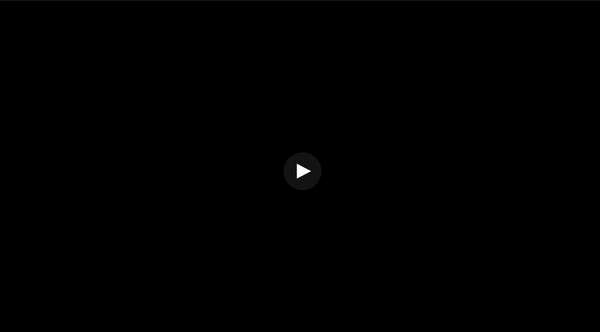
We will be using MountainCar-v0 environment in our code as it is pretty simple to understand and has only 3 possible actions as follows:

0 - the car does nothing
1 - the car moves left
2 - the car moves right

Our goal is to make the car learn to reach the flag. In this problem, the car gets a negative reward for all other states and 0 reward when it reaches the flag.

Before writing the code, let us understand some gym commands.

1. gym.make –> used for creating an environment

2. environment.observation_space –> the co-ordinates of the agent in the environment

3. environment.action_space –> all the possible actions for the agent

4. environment.step –> takes action as an input and returns a new state, reward and the boolean, done

5. environment.render –> plots the steps taken by the agent

Note: Every environment has an upper limit of number of steps, so if you just leave the agent in some infinite loop, it will stop taking actions after the maximum number of steps. In mountainCar-v0, the maximum number of steps is 200.

We will train our model for some episodes, which is nothing but the number of trails the agent makes and update the q-table after each step it takes.

Last thing to note is that we will be discretizing the observation space as the observation space given in the environment is a continuous one and we need it to discretize so that we can update our q-table.

Let us dive into the coding part now:

import numpy as np
import gym

env = gym.make("MountainCar-v0")

num_actions = env.action_space.n
dis_obs_space_size = [30]*len(env.observation_space.high) 
# you can tweak the dis_obs_space as  rectangular patch also, here its [30,30]
dis_obs_space_winsize = (env.observation_space.high-env.observation_space.low)/dis_obs_space_size

learning_rate = 0.2
episodes = 5000
gamma = 0.9

def cont2Discrete(state):
  dstate = (state-env.observation_space.low)/dis_obs_space_winsize
  return tuple(dstate.astype(np.int))

q_table = np.random.uniform(low=-2, high=0, size=(dis_obs_space_size + [num_actions])) # a 3-D array 

show_every = 1000

for eps in range(episodes):
  show = false
  done = False
  dstate = cont2Discrete(env.reset())
  if(eps%show_every==0):
    show = true
    
  while not done:
    action = np.argmax(q_table[dstate])
    new_state, reward, done, _ = env.step(action)
    new_dstate = cont2Discrete(new_state)
    
    if not done:
      current_qval = q_table[dstate + (action,)]
      max_future_qval = np.max(q_table[new_dstate])
      
      new_qval = (1-learning_rate)*current_qval + learning_rate*(reward+ gamma*max_future_qval)
      
      q_table[dstate+(action,)] = new_qval
    
    elif new_state[0]>=env.goal_position:
      q_table[dstate+(action,)]=0 # 0 is the reward
      
      
    dstate = new_dstate
    if(show):
      env.render()
    

env.close()

I will go through the code quickly:

Firstly, we have created a gym environment. Then we have discretized the observation space into a 30x30 grid. For each episode, we are starting with a random state by doing env.reset, then we are checking whether the new state is the required state or not, if it is not then we are updating the q-value according to the above-given equation and if it is the goal_state, we are updating the q-value with a zero. For every 1000 episodes, we are showing the trace of the car.

I trained the model for 5000 epochs. The agent learned to reach the target between 1000-2000 episodes. The quicker it reaches the flag, the better the model has been trained.

I hope that was an enjoyable blog. Keep Learning, Keep Sharing 😊