How to ___ Variational AutoEncoder ?

With the surfeit of blogs on this page, I decide to add one more to the list today. We will be talking about various terms like AutoEncoders and Variational AutoEncoders and finally implementing the latter one. So, you may have heard about data compression, right? It means nothing but encrypting the data in some form which consumes less memory and is capable of restoring almost everything of it when required. Can we do it through machine learning? Obviously, we can and here comes the time when we discuss about autoencoders. So, let us kick in with our new blog.

What is an AutoEncoder?

So AutoEncoder is a type of neural network which is used to encode the data into a low-dimensional representation(in other words compress the data). It is an unsupervised algorithm in which we take the data, encode into a feature vector of lesser dimension and then try to regenerate the data from the compressed feature vector. So the encoding part of the network is called an Encoder, and the decoding part is called a Decoder which makes it an Encoder-Decoder architecture and since it regenerates the same input, it is named as AutoEncoder. Below is the diagram for an autoencoder.

wskdj

The encoder and the decoder part can be anything like feedforward neural network, a convolutional network or a stack of LSTMs or GRUs based on our use case. In the given figure above, x is the input data, z is the compressed feature vector and x’ is the regenerated input.

What is Variational AutoEncoder?

Variational autoencoder is nothing but a variant of the architecture we discussed above. So what makes it different from a normal autoencoder? Yes, you got it right(the word VARIATIONAL). Variational autoencoder not just learns a representation for the data but it also learns the parameters of the data distribution which makes it more capable than autoencoder as it can be used to generate new samples from the given domain. This is what makes a Variational Autoencoder a generative model. The architecture of the model is as follows:

sjd

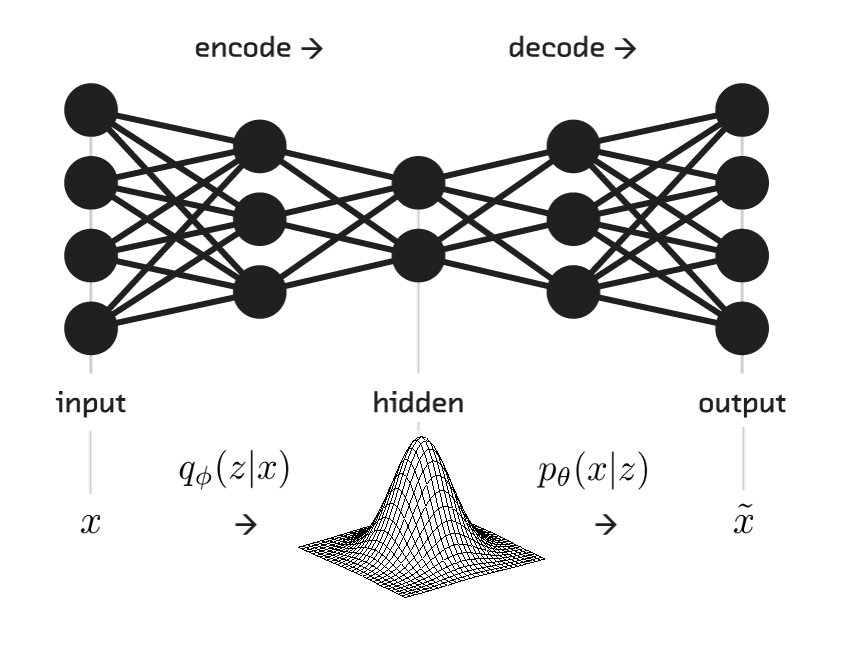
Since a variational autoencoder is a probabilistic model, we aim to learn a distribution for the latent space here(feature representation). A normal autoencoder is very prone to overfitting as it tries to converge the data on a single feature vector and a small change in input can alter the feature vector a lot. To address this issue, we need to use some kind of regularization which restricts the distribution learnt to be far away from each other(minimize the covariance of the latent distributions). We therefore assume the distributions to be close to a normal distribution(mean=0 and variance=1).

We are now good to discuss the loss function of a variational autoencoder. It comprises of two terms:

  1. the reconstruction loss which basically explains the regeneration of the input data
  2. the KL divergence loss which tries to reduce the gap between the distributions learnt with a normal distribution.

The KL divergence loss can be derived as follows:

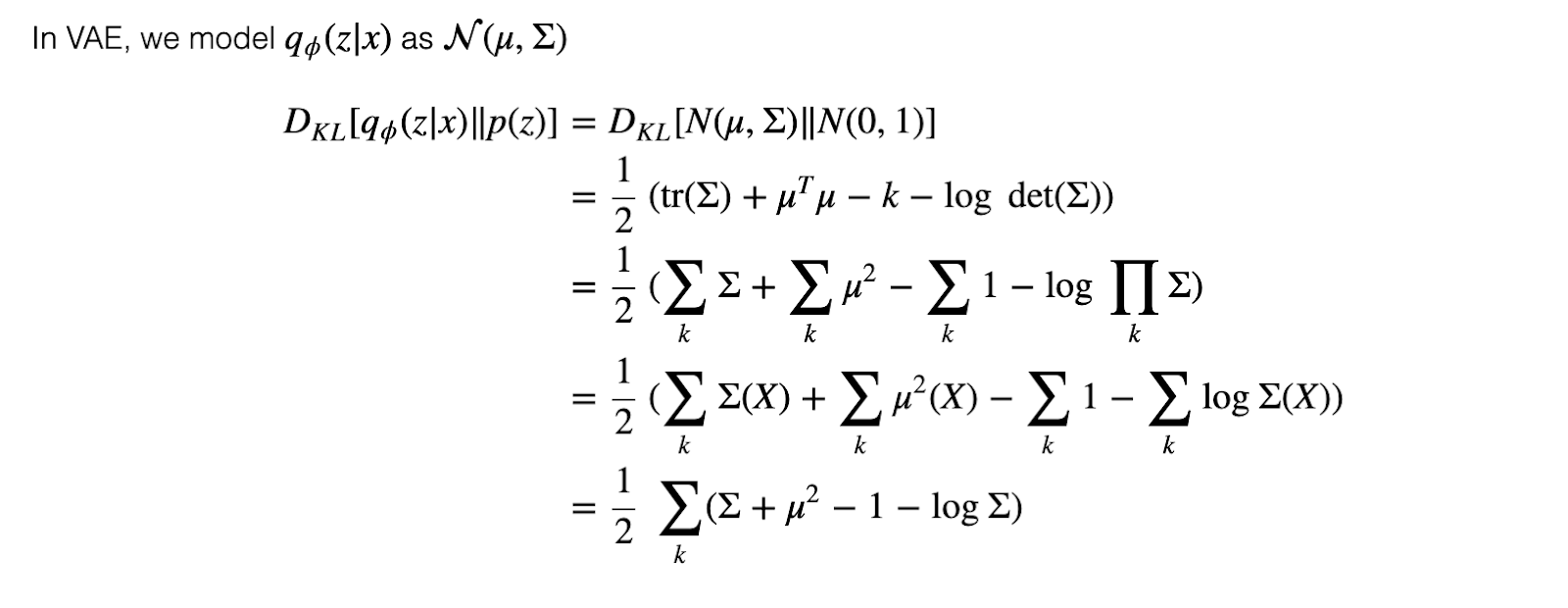
wsldi

The reconstruction loss can be any loss used for supervised algorithms like log loss or mean squared loss. The total loss is the sum of reconstruction loss and the KL divergence loss.

We can summarize the training of a variational autoencoder in the following 4 steps:

  1. predict the mean and variance of the latent space
  2. sample a point from the derived distribution as the feature vector
  3. use the sampled point to reconstruct the input
  4. backpropagate the loss to update the model parameters

Want to build your own VAE

Now that we have pretty much an idea of what autoencoders and variational autoencoders are, let us implement a variational autoencoder using tensorflow and keras:

Necessary Imports

import tensorflow.keras as keras
import tensorflow as tf
import numpy as np
import keras.layers as L
import keras.backend as K

Sampling class

class sampling(L.Layer):
    def __init__(self, intdim, **kwargs):
        self.intdim = intdim
        super(sampling, self).__init__(**kwargs)

    def call(self, args):
        z_mean, z_log_sigma = args
        batch_size = tf.shape(z_mean)[0]
        epsilon = K.random_normal(shape=(batch_size, self.intdim),
                                  mean=0., stddev=1)
        return z_mean + z_log_sigma * epsilon

    def compute_output_shape(self, input_shape):
        return input_shape[0]

    def get_config(self):
        config={'intdim':self.intdim}
        return config

Variational AutoEncoder Class

class VAutoEnc():
    def __init__(self, featurelen, intdim):
        self.vocab_len = vocab_len
        self.featurelen = feature_len
        self.intdim = intdim
        self.sample = self.sampling(self.intdim)
        self.model = self.RetGraph()


    def RetGraph(self):
        encinp = L.Input(shape=(self.featurelen,1), dtype='float64')
        
        l = L.Dense(self.intdim)(encinp)

        mean = L.Dense(self.intdim)(encinp)
        log_sigma = L.Dense(self.intdim)(encinp)

        z   = self.sample([mean, log_sigma])

        out = self.Dense(self.featurelen)(z)
        
        meansigma = L.concatenate([mean, log_sigma], name='meansigma')



        model = keras.models.Model(encinp, [z_l, meansigma])

        return model


    def recloss(self):
        def loss1(y_true, y_pred):
            reconstruct_loss = tf.keras.losses.MSE(y_pred, y_true)
            return reconstruct_loss
        return loss1

    def vaeloss(self):
        def loss2(y_true, y_pred):
            mean = y_pred[:,0:self.intdim]
            log_sigma = y_pred[:, self.intdim:]
            kl_loss = -0.5*K.mean(1+log_sigma-K.square(mean)-K.exp(log_sigma))
            return kl_loss

The code is very simple and plain to understand where we are taking a input vector of featurelen dimension and encoding it to a intdim length latent vector. The reconstruct and kl losses are defined separately. A different sampling layer is defined to sample the data using the mean and variance of the distribution.

Thus we come to the end of the discussion. Hope you liked it. Keep Learning, Keep Sharing