• The Diffusion Process:
• Reversing the Diffusion: Denoising
• Synthesizing New Data: Image Generation from Pure Noise
• Harnessing Text: Conditional Image Generation
• The Advantages of Diffusion Models: Quality, Diversity, and Stability
• Diving into the Mechanics of Diffusion Models
  • Forward Diffusion:
  • Reverse Diffusion:
  • The Loss Function: Guiding the Denoising Symphony
  • Time Embeddings: Providing Temporal Context
• The Mathematical Elegance of Diffusion Models
• Demonstrating Diffusion with the Swiss Roll Distribution
  • The Swiss Roll Distribution: An Overview
  • Training a Small Diffusion Network
  • Results and Insights
• Conclusion
• References

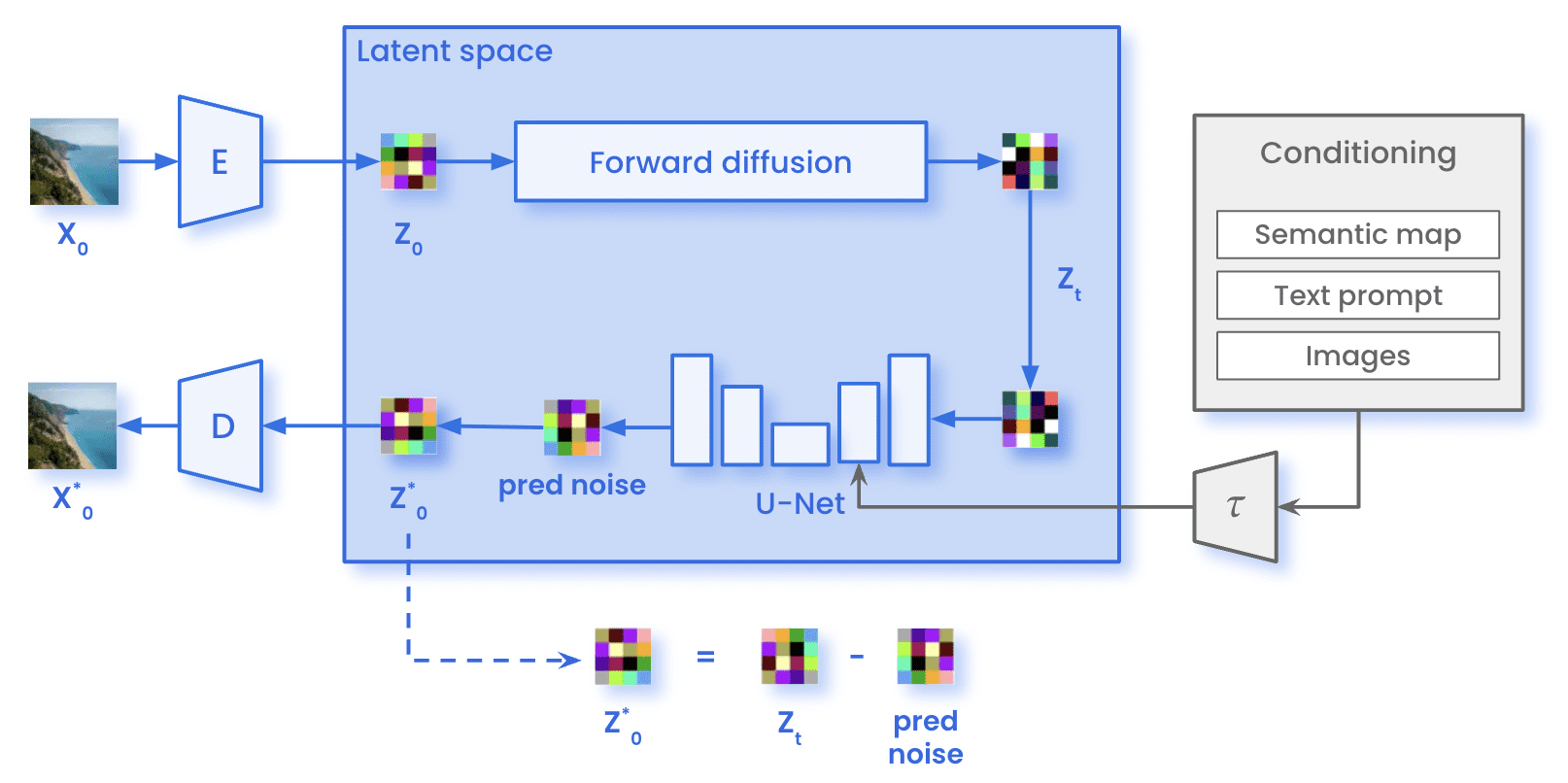
Diffusion models are rapidly emerging as a dominant force in the field of generative artificial intelligence, showcasing an unparalleled ability to synthesize high-quality, diverse images. Unlike previous generative approaches like Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs), Diffusion Models employ a unique two-stage process that leverages the controlled introduction and removal of noise to learn complex data distributions.

The Diffusion Process:

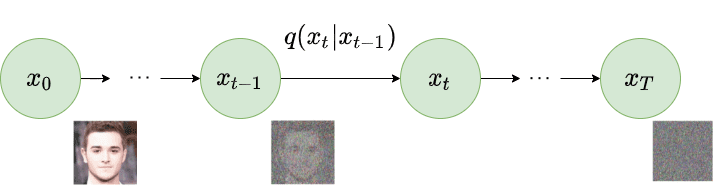
Diffusion models begin by systematically corrupting input data, such as images, through a process termed forward diffusion. This involves the iterative addition of Gaussian noise, following a predefined variance schedule that dictates the amount of noise injected at each timestep. The process continues until the data is transformed into a sample of pure, unstructured noise, effectively obscuring the original information.

Reversing the Diffusion: Denoising

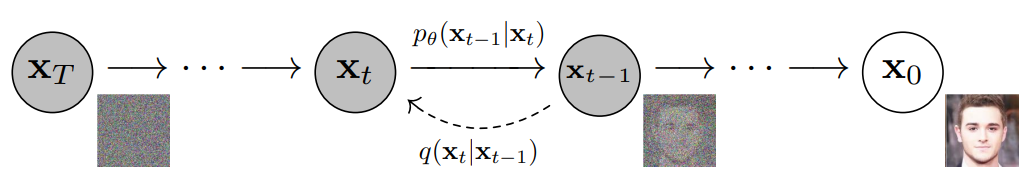
Central to diffusion models is the ability to reverse this noise injection process. A dedicated neural network, often a U-Net, is trained to predict the specific noise pattern added at each timestep. By subtracting the predicted noise from the corrupted data, the model gradually denoises the image, progressively recovering its original structure and detail. This iterative refinement allows the model to capture intricate relationships within the data distribution, resulting in remarkably realistic and varied outputs.

Synthesizing New Data: Image Generation from Pure Noise

The image generation process begins with a tensor of pure random noise, representing a blank slate. This noise is passed through the trained U-Net, which, conditioned on the final timestep of the forward process, predicts the noise present. Subtracting this predicted noise initiates the reverse diffusion, moving one step closer to a cleaner image. This iterative procedure continues, progressively denoising the image at each timestep, until a final, generated image emerges. The result is a novel image that reflects the learned data distribution, exhibiting remarkable fidelity and diversity.

Harnessing Text: Conditional Image Generation

Beyond unconditional generation, Diffusion Models demonstrate a powerful capacity for conditional image generation, guided by textual descriptions. This involves transforming the textual prompt into a text embedding using a language model, typically a transformer-based architecture. This embedding encapsulates the semantic meaning of the description, providing the U-Net with contextual information.

During the denoising process, this text embedding is incorporated to condition the U-Net’s predictions. The model learns to predict noise patterns that align with the textual description, effectively guiding the generation towards images that correspond to the given prompt. Various techniques, including concatenation, cross-attention, and modulation, can be employed to integrate the text embedding into the U-Net architecture.

The Advantages of Diffusion Models: Quality, Diversity, and Stability

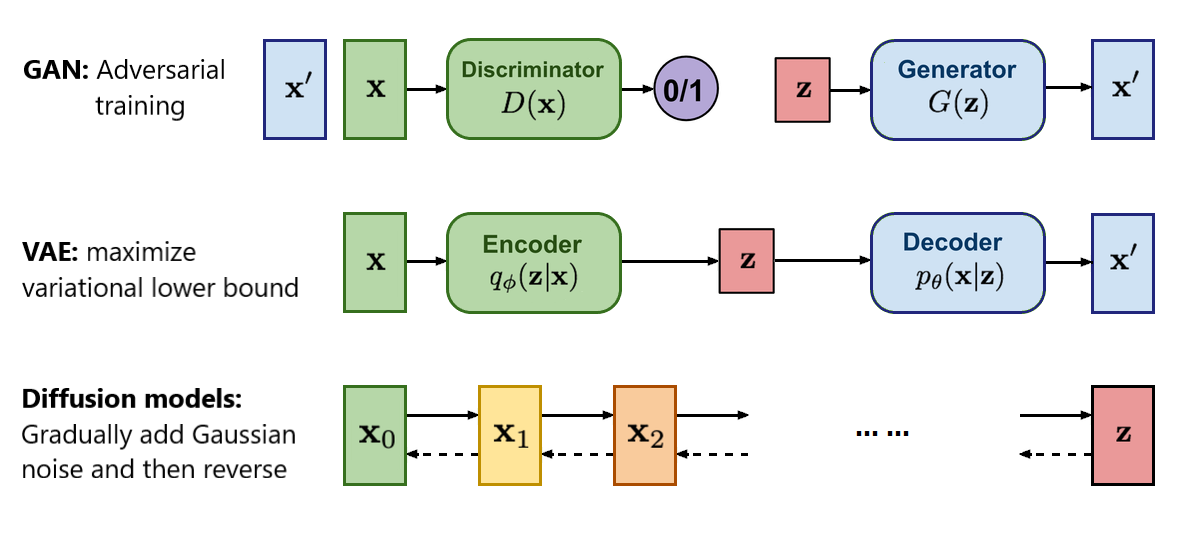
Diffusion Models exhibit several compelling advantages over traditional generative approaches:

• Exceptional Sample Quality and Diversity: Diffusion models have consistently demonstrated the ability to generate images with remarkable fidelity and realism, often surpassing the performance of GANs. Their ability to learn the nuanced structure of data distributions allows for the generation of diverse samples that accurately reflect the variety within the training data. This is further enhanced by their aptitude for conditional generation, enabling the creation of tailored images guided by textual descriptions.
• Robust and Stable Training: Compared to the often-challenging training process of GANs, Diffusion Models offer a significantly more stable and predictable training experience. They are less susceptible to issues like mode collapse and vanishing gradients, making them a more accessible and reliable option for researchers and practitioners.

While the iterative nature of the sampling process can lead to slower generation speeds compared to VAEs and GANs, the compelling advantages in image quality, diversity, and training stability solidify Diffusion Models as a groundbreaking force in generative AI. With ongoing research exploring new variants and applications, the potential of these models to reshape the landscape of image generation and beyond is truly remarkable.

Diving into the Mechanics of Diffusion Models

While the conceptual framework of diffusion models might seem intuitive, their inner workings are underpinned by an elegant mathematical foundation. To truly appreciate their capabilities, we will explore the probability distributions and Markov chains behind diffusion models, understanding the equations that define the diffusion and denoising processes.

Forward Diffusion:

The forward diffusion process can be formalized as a Markov chain, a sequence of random variables where each step depends solely on the preceding one. Given an initial data point $x_0$, we iteratively sample noisy versions of the data by adding Gaussian noise according to the following equation:

\[q(x_t \mid x_{t-1}) = N(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I)\]

where:

• $x_t$ represents the noisy data point at timestep $t$.
• $x_{t-1}$ is the data point at the previous timestep.
• $\beta_t$ is the variance schedule parameter at timestep $t$, controlling the noise level.
• $N(x_t; \mu, \Sigma)$ denotes the Gaussian distribution with mean $\mu$ and covariance matrix $\Sigma$.
• $I$ is the identity matrix.

This equation essentially states that the noisy data point at time $t$ is sampled from a Gaussian distribution whose mean is a scaled version of the previous data point and whose variance is determined by the variance schedule. As we progress through the timesteps, the influence of the original data point diminishes while the noise component dominates, ultimately leading to a sample $x_T$ that is essentially pure Gaussian noise.

Beta (β) - The Variance Schedule:

• $\beta_t$ represents the variance of the Gaussian noise added at timestep t. It’s a value between 0 and 1, where:
  • $\beta_t$ close to 0 means adding very little noise.
  • $\beta_t$ close to 1 means adding a lot of noise, making the data almost completely random.
• The schedule defines how $\beta_t$ changes over time. Common schedules include:
  • Linear: $\beta_t$ increases linearly from a small value to a larger value.
  • Cosine: $\beta_t$ follows a cosine function, allowing for a smoother transition of noise levels.
  • Other: Various other schedules can be designed to control the noise injection process.

Alpha (α) - Signal Retention:

• $\alpha_t = 1 - \beta_t$ represents the amount of signal (original data) we retain at timestep t.
• It’s the complement of the noise variance.

Alpha Bar (ᾱ) - Cumulative Signal Retention:

represents the cumulative product of alphas up to timestep t. It signifies the total fraction of the original signal remaining after t steps of noise addition.

The Diffusion Equation:

The equation governing the forward diffusion process at timestep t is:

\[x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon\]

where:

• $x_t$ is the noisy data point at timestep t.
• $x_0$ is the original data point.
• $\epsilon$ is randomly sampled Gaussian noise from $\mathcal{N}(0, I)$.

Explanation:

• The equation blends the original data ($x_0$) with Gaussian noise ($\epsilon$).
• The weighting of the original data and the noise is controlled by $\bar{\alpha}_t$:
  • At the beginning (t=0), $\bar{\alpha}_t$ is close to 1, meaning we retain most of the original signal.
  • As t increases, $\bar{\alpha}_t$ gets smaller, reducing the influence of the original data and increasing the noise contribution.
  • When t reaches the final timestep (T), $\bar{\alpha}_t$ is very close to 0, resulting in an $x_T$ that is almost entirely noise.

Intuition:

• Beta: Controls the “strength” of the noise added at each step.
• Alpha: Represents how much of the original signal we preserve at each step.
• Alpha Bar: Tracks the total signal preservation across all timesteps up to t.

Why Cumulative Alphas (ᾱ)?

• Efficient Computation: Instead of iteratively adding noise at each step, we can directly sample $x_t$ for any arbitrary timestep t using the formula with $\bar{\alpha}_t$. This significantly speeds up the diffusion process.
• Control over Signal Decay: $\bar{\alpha}_t$ provides a clear measure of how much information from the original data is still present in the noisy sample at timestep t.

By carefully designing the variance schedule ($\beta_t$) and understanding the roles of $\alpha$ and $\bar{\alpha}$, we can precisely control the diffusion process, ensuring a smooth transition from data to noise while retaining enough information for the reverse process to learn effectively.

Reconstructing the Data:

To recover the original data ( x_0 ) from the noisy data ( x_t ) at timestep ( t ), given the noise ( \epsilon ), use the following formula:

\[x_0 = \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \cdot \epsilon}{\sqrt{\bar{\alpha}_t}}\]

Key Points:

• Knowledge of Noise: This formula relies on knowing the exact noise added at timestep t ($\epsilon_t$). During training, we have this information since we sampled the noise ourselves. However, during image generation, we don’t know this noise, so the model has to predict it.
• Iterative Denoising: By applying this formula repeatedly, starting from the final timestep (T) and moving backward to timestep 0, we can progressively remove noise and reconstruct the original data point.

Reverse Diffusion:

The reverse process, denoising, aims to learn the reverse transition probabilities $p_\theta(x_{t-1} \mid x_t)$, parameterized by a neural network with parameters $\theta$. This network, typically a U-Net, takes the noisy image $x_t$ and the timestep $t$ as input and outputs a prediction of the noise added at that timestep.

The reverse process is also modeled as a Markov chain, where each step involves removing the predicted noise from the current image to obtain a less noisy version. However, unlike the forward process, the variance of the noise in the reverse process is fixed, simplifying the mathematical formulation.

The Loss Function: Guiding the Denoising Symphony

Training the diffusion model involves optimizing the parameters $\theta$ of the neural network to minimize a specific loss function. A common choice is a simplified version of the variational lower bound, commonly used in VAEs. This simplified loss function minimizes the L2 distance between the predicted noise and the actual noise added to the image during the forward process at a given timestep.

This loss function can be expressed as:

\[L(\theta) = \mathbb{E}_{t, x_0, \epsilon} \left[ \|\epsilon - \epsilon_\theta(x_t, t)\|^2 \right]\]

where:

• $\epsilon$ represents the actual noise added to the image $x_0$ at timestep $t$.
• $\epsilon_\theta(x_t, t)$ is the noise predicted by the neural network with parameters $\theta$ given the noisy image $x_t$ and timestep $t$.

By minimizing this loss, the neural network learns to accurately predict the noise at each timestep, effectively reversing the forward diffusion process and enabling the generation of new images.

Time Embeddings: Providing Temporal Context

Since the U-Net uses shared parameters across all timesteps, it needs a mechanism to differentiate between the varying noise levels at different stages of the diffusion process. This is achieved through time embeddings, where the timestep $t$ is encoded as a continuous vector representation and provided as additional input to the U-Net. Positional embeddings used in transformers have been used to represent time steps in Diffusion Models as well in recent works. This embedding allows the network to adjust its behavior based on the temporal context, ensuring accurate noise prediction at each timestep.

The Mathematical Elegance of Diffusion Models

The mathematical framework of diffusion models, built on probability distributions, Markov chains, and neural network optimization, provides a robust and elegant approach to generative modeling. By systematically corrupting and denoising data, these models capture the intricate structure of complex data distributions, enabling the generation of high-quality, diverse samples, and even conditional image generation guided by textual descriptions.

Demonstrating Diffusion with the Swiss Roll Distribution

After delving into the mathematical intricacies of diffusion models, let’s put theory into practice with a classic example: the Swiss roll distribution. This example provides a clear and intuitive demonstration of how diffusion models can reconstruct complex structures from noise.

The Swiss Roll Distribution: An Overview

The Swiss roll is a well-known synthetic dataset used for dimensionality reduction and manifold learning. Imagine a two-dimensional flat sheet of dough that is rolled into a cylinder and then unrolled into a spiral shape. This spiral structure, when viewed in three-dimensional space, resembles a rolled-up Swiss cheese. For our demonstration, we will use a 2-D version of the Swiss roll to simplify visualization and better illustrate the model’s performance.

Training a Small Diffusion Network

I used the code provided at https://github.com/albarji/toy-diffusion/blob/master/swissRoll.ipynb to train a simple diffusion model for reconstructing a swiss roll distribution from a random noise. The process involves the following key steps:

1. Data Preparation: It starts with a dataset that represents the 2-D Swiss roll distribution. This dataset will serve as our target for the diffusion model to learn.

2. Noise Sampling: Then it uses a cosine scheduler for noise sampling and adding noise to the generated swiss dataset.

3. Model Architecture: The code demonstrates how to design a small diffusion network, which includes a series of linear layers(for Upsampling and Downsampling) and activation functions.

4. Training the Network: The model is trained to learn the reverse process of diffusion. This involves gradually denoising a sample of pure noise until it resembles the 2-D Swiss roll distribution. It uses a MSE loss function which minimizes the difference between the actual noise we sampled and the noise which the model predicted.

5. Diffusion Process: During training, the model learns to simulate the diffusion process in reverse. Starting from pure noise, the network iteratively refines the sample, applying learned transformations to approach the Swiss roll distribution.

6. Evaluation and Visualization: After training, we evaluate the model’s performance by generating samples from the diffusion process. We visualize these samples to assess how well the network has learned to reconstruct the 2-D Swiss roll distribution in 40 diffusion steps starting from a pure noise.

Results and Insights

Upon visualizing the results, we expect to see that the diffusion network effectively transforms random noise into a well-defined 2-D Swiss roll distribution. This demonstrates the model’s ability to capture and generate complex structures from seemingly unstructured input.

Conclusion

This demonstration highlights the power of diffusion models in learning and generating complex data distributions. By starting from pure noise and training on a classic dataset like the Swiss roll, we can visualize the efficacy of these models in reconstructing and understanding complex data structures. Diffusion Models are revolutionizing the way we generate content with AI. Tools like DALL-E 3 and stable diffusion are already showcasing their ability to create stunning visuals from textual descriptions.

But the potential of Diffusion Models extends far beyond image creation! Their proficiency in understanding and generating various forms of data has researchers exploring their use in exciting new areas, such as music generation, voice generation or even cinematic video generation etc.

What fascinating advancements might we see in the future?

• Multisensory experiences: Envision AI creating experiences that blend sight, sound, and even touch!
• Personalized creations: Picture AI crafting music that resonates with your mood, artwork that mirrors your style!

While Diffusion Models are still in their early stages, their potential is immense! They could transform how we create and experience a wide array of content in the future.

References

1. https://www.youtube.com/watch?v=a4Yfz2FxXiY
2. https://arxiv.org/pdf/2102.09672
3. https://github.com/albarji/toy-diffusion/blob/master/swissRoll.ipynb